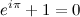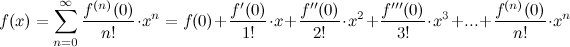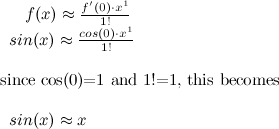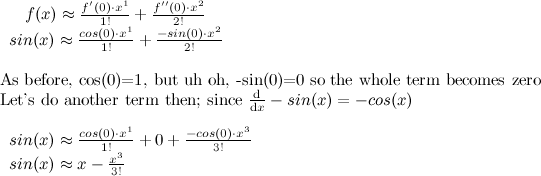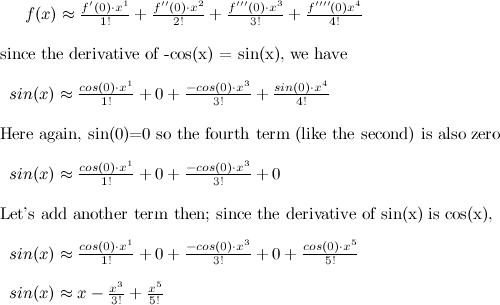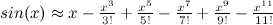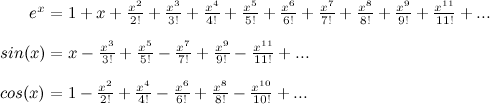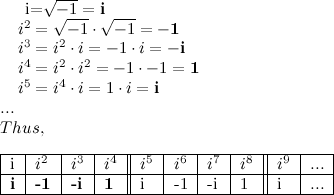"The Greatest Equation of All Time"

Sorry to have been so long away from the blog! The purpose of this post is to give some intuition for Euler's identity, "the most beautiful theorem in mathematics", to those who haven't seen it before or to those for whom it is meaningless because they lack the mathematical background.

It was never introduced to me in any class, and unless you majored in math or physics the same is probably true for you. I wanted not only to call your attention to this equation, but also to derive it, the derivation of which is equally marvellous. Walking through the derivation with a pencil was perhaps my first real taste of what I imagine mathematicians live and breathe for; my present aim is to give you a taste!

Here it is:

It's pretty astounding when you look at it for the first time... it seems a ridiculous assertion! (However, Gauss is supposed to have said that if this was not immediately apparent to you on being told it, you would never be a first-class mathematician.) He also had a really cool signature, so he is probably right.

Really though? Are we talking about e (2.71828...), like from continuously compounded interest? You mean π (3.14159...), like a circle's circumference-to-radius ratio? And the imaginary number i, the square root of -1, that we talked about for like a week in high school and then never actually used for anything? Yep, those are the ones, e, π, and i. Dust off your old TI-8x, punch this badboy in, and see what output you get. The batteries are probably dead so I'll spare you the trouble:

Though I am mainly interested in showing you a way to get to this shocking identity, I will need thereby to talk a bit about Taylor series approximations. If you don't know much about this technique, think of using a sum of polynomials to approximate the shape of function at a given point. If you don't know much about polynomials and functions, think of adding together easy-to-compute things (x, x², x³, ...) to approximate hard-to-compute things (e^x, sin(x), ln(x), ...). This is actually how your calculator computes with things like e, π, et al. 

But this isn't a post about Taylor series approximations, so I'll cut down on the details. If you already understand how to use Taylor series approximations, you could skip to the derivation. If you aren't, it is super useful and cool, so check it out! First things first: if you want to approximate the shape of a function f(x) using an easier-to-work-with polynomial like a power series (i.e., a + bx + cx² + dx³ ... where a, b, c, d,... are constants), you can do it like this:

where f⁽ⁿ⁾(0) represents the nth derivative of function f(x), evaluated at x=0 (this gives us the shape around x=0) Technically, this is a Maclaurin series. Really cool! Because if we can keep taking derivatives, we can get an almost perfect approximation of f(x) using polynomials instead. Don't worry, I'm not going to ask you to do any calculus (though you might want a helpful refresher on derivatives*). I'll just show you the results.

To follow the derivation, you just need the following 3 results: the derivative of sin(x) is cos(x), the derivative of cos(x) is -sin(x), and the derivative of e^x is itself, just e^x.

Let's do sin(x) first, because I've got some pretty pictures of it!

We want to approximate this function using a Taylor series polynomial. Let us do so by taking the first term of that big equation above:

So using only 1 term, our approximation is the line y=x

Not a very satisfying approximation, is it? What about 2 terms?

If we plot x - x³/3!, we get

Hey wow, that's a lot better! The polynomial x - x³/3! seems to pretty exactly mimic sin(x), at least around x=0. Let's add another term.

Now our approximation is y = x - x³/3! + x⁵/5! which looks like this:

Even better! You can see that by adding more terms of the Taylor polynomial, we get a closer approximation of the original function. Here's a couple more terms just to illustrate:

Now the polynomial approximation is virtually indistinguishable from sin(x), at least at from x=-pi to x=pi. Here's a more "moving" display of this (credit). Notice how adding more and more terms gets us an ever-better approximation of sin(x).

Here's an even easier example! (We are going to need this result too.)

So we have Taylor series approximations for sin(x) and for e^x. Now all we need is one for cos(x). It is just like sin(x) except all of the opposite terms cancel out! I'll leave this as an exercise to the reader (always wanted to say that!) and just give you the result:

Take a minute to look at these. Strange, isn't it? If it weren't for those negative signs, it looks like simply adding sin(x) and cos(x) would give us e^x... Hmmm.

We are now in a position to make some magic happen, but one more thing remains to be done. Now's the time to recall your imaginary number i, which is equal to √−1. Since i = √−1, we know i² = -1. For higher powers of i, we have the following pattern:

The pattern i, -1, -i, 1, repeats as you take ever higher powers of i. Notice that the signs are switching too! You should be excited about this. Now we're ready for the main event!



YEAH! WOOHOO! At least, that's how I felt when I first saw it.

And it's not just superficially beautiful either. Before we plugged in pi, we saw that e^ix=cos(x) + i*sin(x). This formula has many important applications, including being crucial to Fourier analysis. For an excellent introduction, check this out.

Well, I hope that if the derivation didn't leave you reeling in perfect wonderment, you were at least given something to think about! Thanks for reading!
________________________________________________________________
*Quick derivatives refresher
It may be helpful to think of the derivative of a function f(x)---symbolized as d/dx f(x) or f'(x)---as a machine that gives of the slopes of tangent lines anywhere along the original function: if you plug x=3 into f'(x), what you get out is the slope of a line tangent to the original function f(x) at x=3. Since slope is just rise-over-run, the rate at which a function is increasing or decreasing, the derivative gives as the rate at which the original function is increasing or decreasing at a single point. If f(x) is the parabola x2, then its derivative f'(x) is 2x. At x=0, the very bottom of the parabola, we get f'(0)=2(0)=0, which tells us the line tangent to x2 at the point x=0 has zero slope (it's just a horizontal line). At x=1, the parabola has started to increase; the rate it is increasing at that point (the slope of the line tangent to that point) is f'(1)=2(1)=2; so now we have a line that goes up 2 for every 1 it goes over. At f'(2)=2(2)=4, a line that goes up 4 for every 1 it goes over. This agrees with our intuition when we look at a parabola; it is accelerating upward at an ever increasing rate.

"Important Peculiarities" of Memory

In my high school psychology class I was told that human memory capacity was unlimited ...and it has bothered me ever since. How, I mean? Aside from the physical limitations on information storage, how could a system that remembers everything forever be evolutionarily advantageous?

This is a question I hope to explore in a deeper way sometime soon; for now, I want to talk to you about a few "peculiarities of human memory" that begin to shed some light on the situation (Bjork & Bjork, 1992). Know that I am drawing heavily from this source and their Theory of Disuse for the present discussion. This is really the coolest part, but I've left it until the end. First, let's talk about three "peculiarities"...

1. STORAGE AND RETRIEVAL ARE TWO DIFFERENT THINGS:
Analogies of human memory -- to a bucket being filled, to computer memory, to magnetic tape -- are often grossly misleading. No literal copy is recorded when you store a piece of information in memory. Learning isn't opening a drawer and putting something in; remembering isn't opening a drawer and taking something out. Indeed, your brain is not a drawer.

New things are placed into memory via their semantic connections to things already in long-term memory. The more knowledge you have of a given area, the more ways you have to store additional information about it. This is a strange biological instantiation of the Matthew effect, where "the rich get richer". To me, one of the most incredible things about being a living, thinking human is this virtually unlimited capacity for storing new information. And when I say "incredible," I mean it both in the sense of "wow, golly!" as well as in the more literal sense of "not credible."

"But wait," I hear you ask, "if my memory is so bally infinite, why can't I remember my passwords half the time? And I'm always forgetting peoples' names, and I can't remember a single word of that book I read last week, and..." As it turns out, getting information into memory is easy, but getting it out is quite another matter.

Quick, what was your childhood address? Your first cellphone number? Your seventh grade math teacher's name? Your high school ID card number? How about your old AIM password? Even the most repetitively drilled, frequently accessed pieces of information eventually become inaccessible through years of disuse. Weirdly though, this information is still stored in memory: you could probably correctly identify each of the above from a list of distracters, for example, and you probably wouldn't have any trouble remembering if you were back in the context of your home town. Perhaps if I had asked you on a different day, when you were in a different mood or frame of mind, you would've been able to retrieve the information. Often information that is effortlessly recallable on one occasion can be impossible to recall on another. Maybe you weren't able to muster the answers at first, but now after expending a bit of time and effort you have remembered. Should the old information become pertinent again, it will certainly be relearnable at an accelerated rate.

What we can and cannot retrieve from memory at any given time appears to be a function of the cues that are available to us at that time. These "cues" may be general situational factors (environmental, social, emotional, physical) as well as those having a direct relationship to the to-be-retrieved item. Cues that were originally associated in storage with the target item need to be reinstated (physically, mentally, or both) at the time of retrieval.

The main takeaway here is that our capacity for storage is far greater than our capacity for retrieval, and it appears that fundamentally different processes are responsible for each. Storage strength represents how well an item is learned, whereas retrieval strength indexes the current ease of access to the item in memory. These two strengths are independent: Items with high retrieval strength can have low storage strength (e.g., your room number during a 5-day stay at a hotel).

2. RETRIEVAL MODIFIES THE MEMORY!
The mechanical analogies have other flaws; reading from computer memory does not alter the contents, whereas the act of retrieving information in human memory modifies the system. When you remember something, that piece of information becomes easier to remember in the future (and other information becomes less retrievable). This is why taking tests is better for long-term retention than studying is. More odd is the idea that recalling Thing A can make it more difficult to recall Thing B in the future, an effect sometimes known as "retrieval competition." This topic is very, very interesting but that's all I'm going to say about it here. For more on the testing effect, check out this paper.


3. LONG-HELD MEMORIES ARE HARD TO REPLACE
Through disuse, then, things become hard to retrieve. But oddly, the earlier the memory was constructed (i.e., the older it is), the more easy it is to access relative to related memories constructed later. Say you decide to change your email password; after doing so, the new password will be the most readily accessible of the two. If you use it to log in tomorrow, you will have little trouble recalling it. However, if you do not have occasion to use either password for a while (new or old), the old password becomes far easier to remember relative to the new password.

Consider athletes: a long layoff often leads to the recovery of old habits. This can help an athlete recover from a recent funk, or it can be a major setback for a rookie who has been rapidly improving. In occupational settings too, and even the armed services, people can appear to be well-trained but then turn around and take inappropriate actions at a later time (i.e., fall back on old habits), particularly in stressful situations. It may even result in the unreasonable surprise we often feel when we see that a child has grown, or a friend has aged, or a town has changed; perhaps we are overestimating these changes because our memory of the child, friend, or town is biased toward a past version of them stored more securely in memory.

This stuff has firm support from laboratory studies too, but I don't want to bore with great detail. Suffice it to say that, if experimental subjects are given a long list of items to memorize and then afterwards asked to recall all of the times that they can remember, there will be a strong recency effect: the items later in the list will be more easily recalled. If, later on (say a day or a week later), subjects are asked to recall all of the items they can remember, there will be a strong primacy effect: the items appearing first will be better recalled than the items appearing later. That this, with the passage of time there is a change from recency to primacy. This finding holds across different delays, tasks, materials, and even species (Wright 1989)!


The Theory of Disuse:
In brief, Bjork and Bjork's (1992) theory states that items of information, no matter how retrievable or well-stored they are in memory, will eventually become nonrecallable if they are not used enough. This is not to say that the memory has decayed or been deleted... it is just inaccessible. Storage and retrieval are two very different things; storage strength reflects the how well-learned the item is, while retrieval strength represents how easy it is to access the item. Unlike storage capacity, retrieval capacity is limited; that is, there are only so many items that are retrievable at any given time in response to a cue or set of cues. As new items are learned, or as the retrieval strength of certain items in memory are increased, other items become less recallable. These competitive effects are generally determined by category relationships defined semantically or episodically; that is, a given retrieval cue (or cues) will define a set of associated items in memory, and the dynamics of competition for retrieval capacity take place across the set.

The theory makes many predictions that account for those peculiarities stated above. Retrieval capacity is limited, not storage capacity, and the loss of retrieval access is not a consequence of the passage of time per se, but of the learning and practice of other items. Retrieving an item from memory makes it easier to retrieve that item in the future but makes it more difficult to retrieve other associated items. The theory also explains why overlearning (additional learning practice after perfect performance is achieved) slows the rate of subsequent forgetting: perfect performance is a function of retrieval strength (which cannot go beyond 100%), whereas additional learning practice continues to increase storage strength. Finally, the spacing effect--the fact that spreading out your study sessions is far more effective for long-term retention than is cramming--can be accounted for by the theory as well. Spacing out repetitions increases storage strength to a greater extent than does cramming, which in turn slows the rate of loss of retrieval strength, thereby enhancing long-term performance. Importantly, cramming can still produce a higher level of initial recall than that produced by spacing, but like the switch from recency to primacy, the switch happens rather quickly.

Again, to spin an evolutionary just-so story, all of this seems pretty adaptive. It is sensible that the items in memory we have been using lately are the ones that are most readily accessible; the items that have been retrieved in the recent past are those most relevant to our current situation, interests, problems, goals... and in general, those items will be relevant to the near future as well. To keep the system current, it makes good sense that we lose access to information that we have quit using: for example, when telling someone our address, it would not be useful to recall every home address we have had in the past.

I look at all of this and I see a selection process at work. The set of items in memory is like so many species in an ecosystem; introduce a new species, and it will die unless it finds a niche (new information must be learned well enough to make it into long-term memory in the first place). Some species don't have much to do with one another, whereas others are mutually dependent and others in direct competition (increasing the retrieval strength of one item reduces the retrieval strength of other, related items). Species with low fitness diminish relative to those with high fitness because they cannot stay  competitive (the items that are used the most proliferate at the expense of items that don't, the item's fitness being determined by the history and recency of its use). Longer, more established species are better adapted to their environment and thus tend to outcompete newcomers (older, more well-connected items memory are easier to recall than newly learned items lacking a deep connection to other items in memory). Species die out, but rarely go completely extinct; instead, they can emigrate elsewhere. They are still extant, but no longer part of the active ecosystem. When conditions improve and it becomes adaptive to return to the ecosystem again, the species is easily reinstated. My metaphor falls apart in places, but I find the selection scheme a good jumping of point for most discussions of this nature.